What is Deep Learning

Overview
Deep Learning
a type of machine learning based on artificial neural networks in which multiple layers of processing are used to extract progressively higher level features from data.
Machine Learning
development of computer systems that can learn to more accurately predict the outcomes without following explicit instructions, by using algorithms and statistical models to draw inferences from patterns in data.
Differences between Deep Learning and Machine Learning
Machine Learning
uses algorithms to parse data, learn from that data, and make informed decisions based on what it has learned.
needs a human to identify and hand-code the applied features based on the data type. | tries to learn features extraction and representation as well.
tend to parse data in parts, then combined those into a result (e.g. first number plate localization and then recognition).
requires relatively less data and training time
Deep learning
structures algorithms in layers to create an “artificial neural network” that can learn and make intelligent decisions on its own.
tries to learn features extraction and representation as well.
Deep learning systems look at an entire problem and generate the final result in one go (e.g. outputs the coordinates and the class of object together).
requires a lot more data and training time
Applications Of Machine Learning/Deep Learning
Email spam detection
Fingerprint / face detection & matching (e.g., phones)
Web search (e.g., DuckDuckGo, Bing, Google)
Sports predictions
ATMs (e.g., reading checks)
Credit card fraud
Stock predictions
Broad categories of Deep learning

Perceptron
Definition
Simplest artificial neuron that takes binary inputs and based on their weighted sum reaching a threshold, generates a binary output.
Artificial neurons
Takes in multiple inputs and learns what should be the appropriate output
Essentially a mathematical function where the weights multiplied with the inputs are learnable
Acts like a logic gate but the operation performed adjusts according to the data
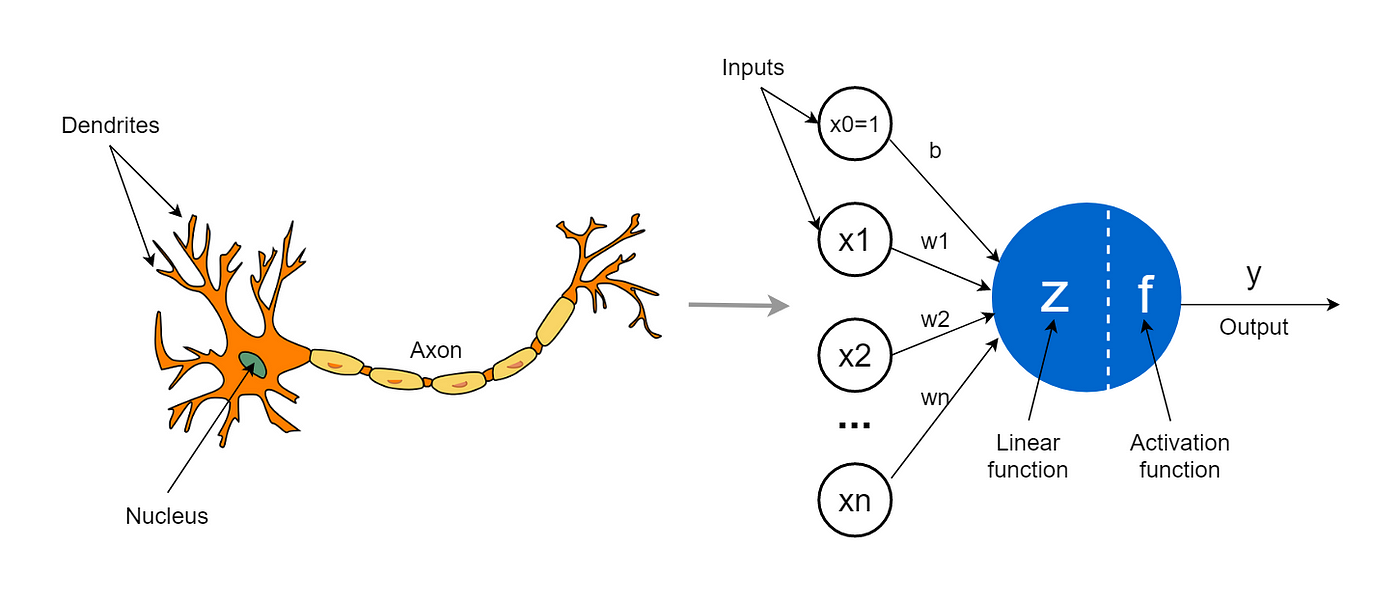
connect them in a network to create an artificial brain(let)
History of the Perceptron
Invented in 1957 by Frank Rosenblatt to binary classify an input data.
An attempt to replicate the process and ability of human nervous system.
A Biological Neuron

McCulloch & Pitts Neuron Model

Computational Model of a Biological Neuron

Terminology
Net input \(=\) weighted inputs, \(z\)
Activations = activation function(net input); \(a=\sigma(z)\)
Label output \(=\) threshold(activations of last layer); \(\hat{y}=f(a)\)
Special cases:
In perceptron: activation function = threshold function
In linear regression: activation \(=\) net input \(=\) output
Often more convenient notation: define bias unit as \(w_0\) and prepend a 1 to each input vector as an additional feature value
Perceptron Learning Algorithm
Let \(\mathcal{D}=\left(\left\langle\mathbf{x}^{[1]}, y^{[1]}\right\rangle,\left\langle\mathbf{x}^{[2]}, y^{[2]}\right\rangle, \ldots,\left\langle\mathbf{x}^{[n]}, y^{[n]}\right\rangle\right) \in\left(\mathbb{R}^m \times\{0,1\}\right)^n\)
Initialize \(\mathbf{w}:=0^m \quad\) (assume notation where weight incl. bias)
For every training epoch:
For every \(\left\langle\mathbf{x}^{[i]}, y^{[i]}\right\rangle \in \mathcal{D}\) :
\(\hat{y}^{[i]}:=\sigma\left(\mathbf{x}^{[i] \top} \mathbf{w}\right)\)
err \(:=\left(y^{[i]}-\hat{y}^{[i]}\right)\)
\(\mathbf{w}:=\mathbf{w}+e r r \times \mathbf{x}^{[i]}\)
Vectorization in Python
Running Computations is a Big Part of Deep Learning!
import torch
def forloop(x, w):
z = 0.
for i in range(len(x)):
z += x[i] * w[i]
return z
def listcomprehension(x, w):
return sum(x_i*w_i for x_i, w_i in zip(x, w))
def vectorized(x, w):
return x.dot(w)
x, w = torch.rand(1000), torch.rand(1000)
%timeit -r 10 -n 10 forloop(x, w)
%timeit -r 10 -n 10 listcomprehension(x, w)
%timeit -r 10 -n 10 vectorized(x, w)
8.64 ms ± 60.2 µs per loop (mean ± std. dev. of 10 runs, 10 loops each)
7.42 ms ± 47.1 µs per loop (mean ± std. dev. of 10 runs, 10 loops each)
The slowest run took 11.05 times longer than the fastest. This could mean that an intermediate result is being cached.
6.61 µs ± 9.7 µs per loop (mean ± std. dev. of 10 runs, 10 loops each)
Perceptron Pytorch Implementation
Label data
import torch
import matplotlib.pyplot as plt
c1_mean , c2_mean = -0.5 , 0.5
c1 = torch.distributions.uniform.Uniform(c1_mean-1,c1_mean+1).sample((200,2))
c2 = torch.distributions.uniform.Uniform(c2_mean-1,c2_mean+1).sample((200,2))
features = torch.cat([c1,c2], axis=0)
labels = torch.cat([torch.zeros((200,1)), torch.ones((200,1))], axis = 0)
data = torch.cat([features, labels],axis=1)
X, y = data[:, :2], data[:, 2]
y = y.to(torch.int)
print('X.shape:', X.shape)
print('y.shape:', y.shape)
X_train, X_test = X[:300], X[100:]
y_train, y_test = y[:300], y[100:]
# Normalize (mean zero, unit variance)
mu, sigma = X_train.mean(axis=0), X_train.std(axis=0)
X_train = (X_train - mu) / sigma
X_test = (X_test - mu) / sigma
plt.scatter(X_train[y_train==0, 0], X_train[y_train==0, 1], label='class 0', marker='o')
plt.scatter(X_train[y_train==1, 0], X_train[y_train==1, 1], label='class 1', marker='s')
plt.title('Training set')
plt.xlabel('feature 1')
plt.ylabel('feature 2')
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.legend()
plt.show()
plt.scatter(X_test[y_test==0, 0], X_test[y_test==0, 1], label='class 0', marker='o')
plt.scatter(X_test[y_test==1, 0], X_test[y_test==1, 1], label='class 1', marker='s')
plt.title('Test set')
plt.xlabel('feature 1')
plt.ylabel('feature 2')
plt.xlim([-3, 3])
plt.ylim([-3, 3])
plt.legend()
plt.show()
X.shape: torch.Size([400, 2])
y.shape: torch.Size([400])


Train and evaluate
import torch
device = torch.device("cuda:0" if torch.cuda.is_available() else "mps")
class Perceptron:
def __init__(self, num_features):
self.num_features = num_features
self.weights = torch.zeros(num_features, 1,
dtype=torch.float32, device=device)
self.bias = torch.zeros(1, dtype=torch.float32, device=device)
self.ones = torch.ones((1, 1), device=device)
self.zeros = torch.zeros((1, 1), device=device)
def forward(self, x):
linear = torch.mm(x, self.weights) + self.bias
predictions = torch.where(linear > 0., self.ones, self.zeros)
return predictions
def backward(self, x, y):
predictions = self.forward(x)
errors = y - predictions
return errors
def train(self, x, y, epochs):
for e in range(epochs):
for i in range(y.shape[0]):
errors = self.backward(x[i].reshape(1, self.num_features), y[i]).reshape(-1)
self.weights += (errors * x[i]).reshape(self.num_features, 1)
self.bias += errors
def evaluate(self, x, y):
predictions = self.forward(x).reshape(-1)
accuracy = torch.sum(predictions == y).float() / y.shape[0]
return accuracy
ppn = Perceptron(num_features=2)
X_train_tensor = torch.tensor(X_train, dtype=torch.float32, device=device)
y_train_tensor = torch.tensor(y_train, dtype=torch.float32, device=device)
ppn.train(X_train_tensor, y_train_tensor, epochs=5)
print('Model parameters:')
print('Weights: %s' % ppn.weights)
print('Bias: %s' % ppn.bias)
X_test_tensor = torch.tensor(X_test, dtype=torch.float32, device=device)
y_test_tensor = torch.tensor(y_test, dtype=torch.float32, device=device)
test_acc = ppn.evaluate(X_test_tensor, y_test_tensor)
print('Test set accuracy: %.2f%%' % (test_acc*100))