Tree Data Structure
Spanning Trees
A spanning tree is a sub-graph of an undirected connected graph, which includes all the vertices of the graph with a minimum possible number of edges. If a vertex is missed, then it is not a spanning tree. The edges may or may not have weights assigned to them.
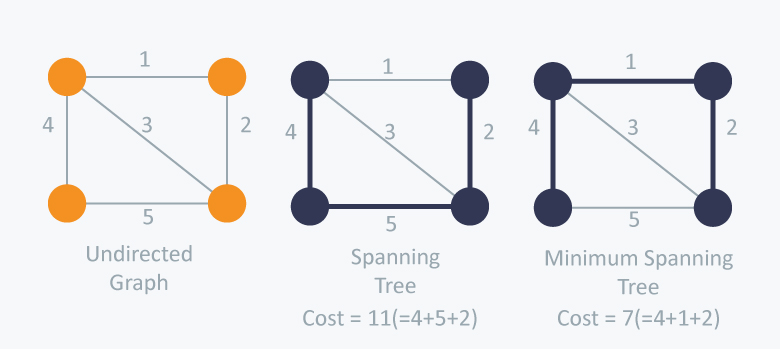
Minimum Spanning Tree
A minimum spanning tree is a spanning tree with the minimum possible sum of edge weights. The edges may or may not have weights assigned to them.

Finding Minimum Spanning Tree
There are many algorithms to find the minimum spanning tree. The most common ones are:
Kruskal’s Algorithm
Prim’s Algorithm
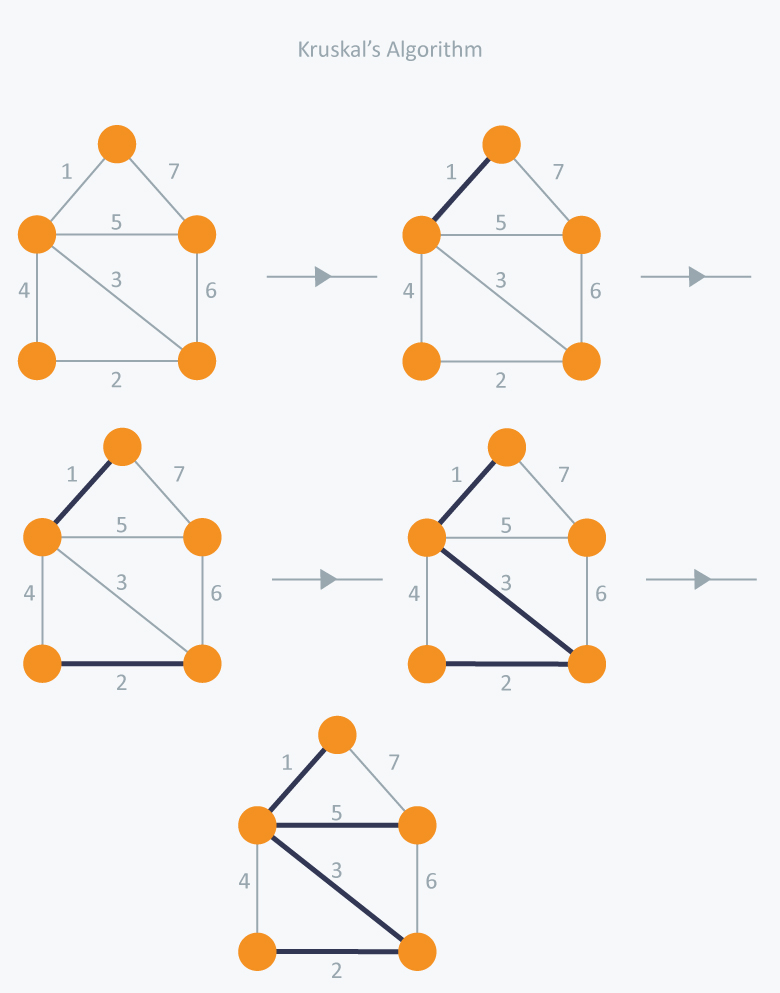
Kruskal’s Algorithm
Kruskal’s algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component).
Algorithm Steps:
Sort the graph edges with respect to their weights.
Start adding edges to the MST from the edge with the smallest weight until the edge of the largest weight.
Only add edges which doesn’t form a cycle , edges which connect only disconnected components.
Union Find Data Structure
Union Find is a data structure that keeps track of a set of elements partitioned into a number of disjoint (non-overlapping) subsets. It supports two operations:
Find: Determine which subset a particular element is in. This can be used for determining if two elements are in the same subset.
Union: Join two subsets into a single subset.
Amortized Analysis
Amortized analysis is a method of analyzing the costs associated with a data structure that averages the worst operations out over time.