Pytorch Fundamental
PyTorch allows you to manipulate and process data and write machine learning algorithms using Python code.
import torch
import numpy as np
torch.__version__
'2.2.2+cu121'
Tensors
Tensors are the fundamental building block of machine learning.
For example, you could represent an image as a tensor with shape [3, 224, 224] which would mean [colour_channels, height, width], as in the image has 3 colour channels (red, green, blue), a height of 224 pixels and a width of 224 pixels.
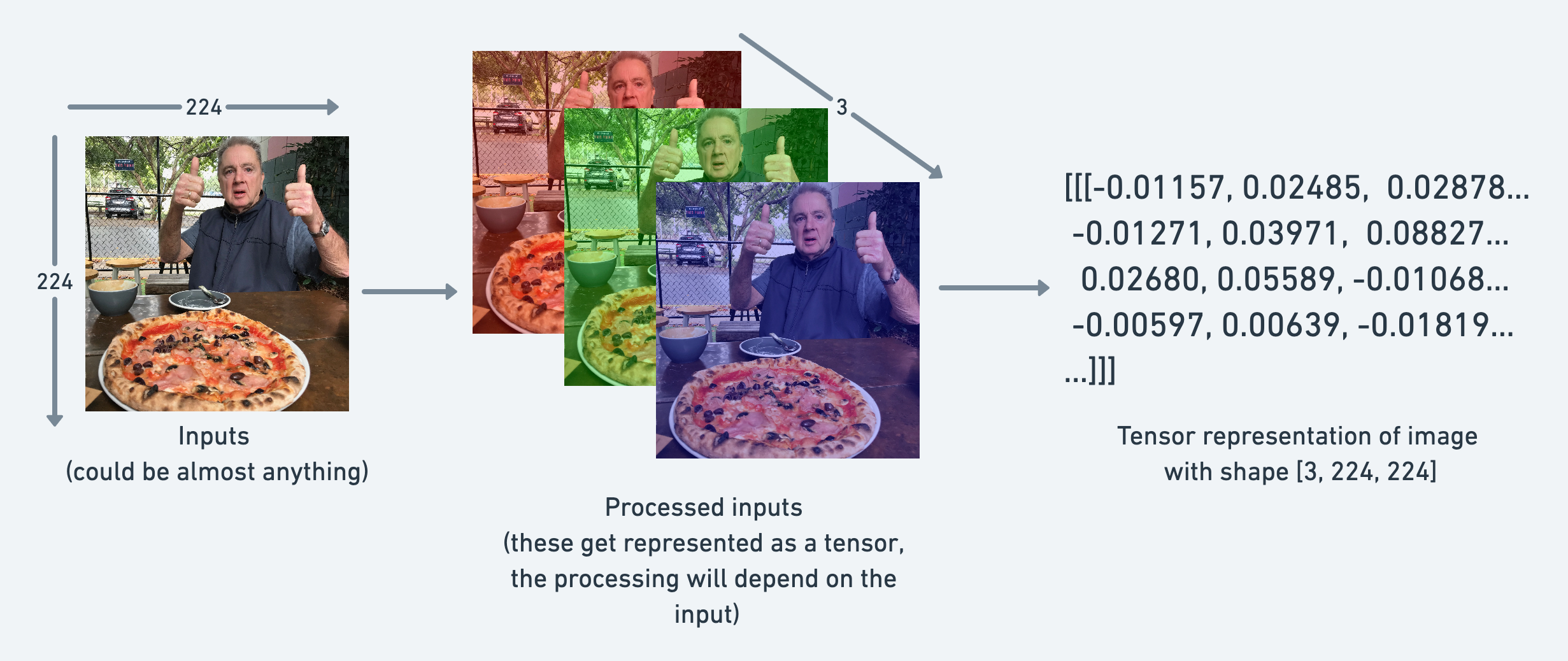
Scalar
# Scalar
scalar = torch.tensor(7)
scalar
tensor(7)
scalar.shape
torch.Size([])
# We can check the dimensions of a tensor
scalar.ndim
0
# If we wan to retrieve the value of a scalar tensor, we can use the .item() method
scalar.item()
7
Vectors
vector = torch.tensor([7, 7])
vector
tensor([7, 7])
# Check the number of dimensions of vector
# You can tell the number of dimensions a tensor in PyTorch has by the number of square
# brackets on the outside ([) and you only need to count one side.
vector.ndim
1
# The shape tells you how the elements inside them are arranged.
vector.shape
torch.Size([2])
Matrix
# Matrix
MATRIX = torch.tensor([[7, 8],
[9, 10]])
MATRIX
tensor([[ 7, 8],
[ 9, 10]])
# Wow! More numbers! Matrices are as flexible as vectors, except they've got an extra dimension.
MATRIX.ndim
2
MATRIX.shape
torch.Size([2, 2])
Tensor
I want to stress that tensors can represent almost anything.
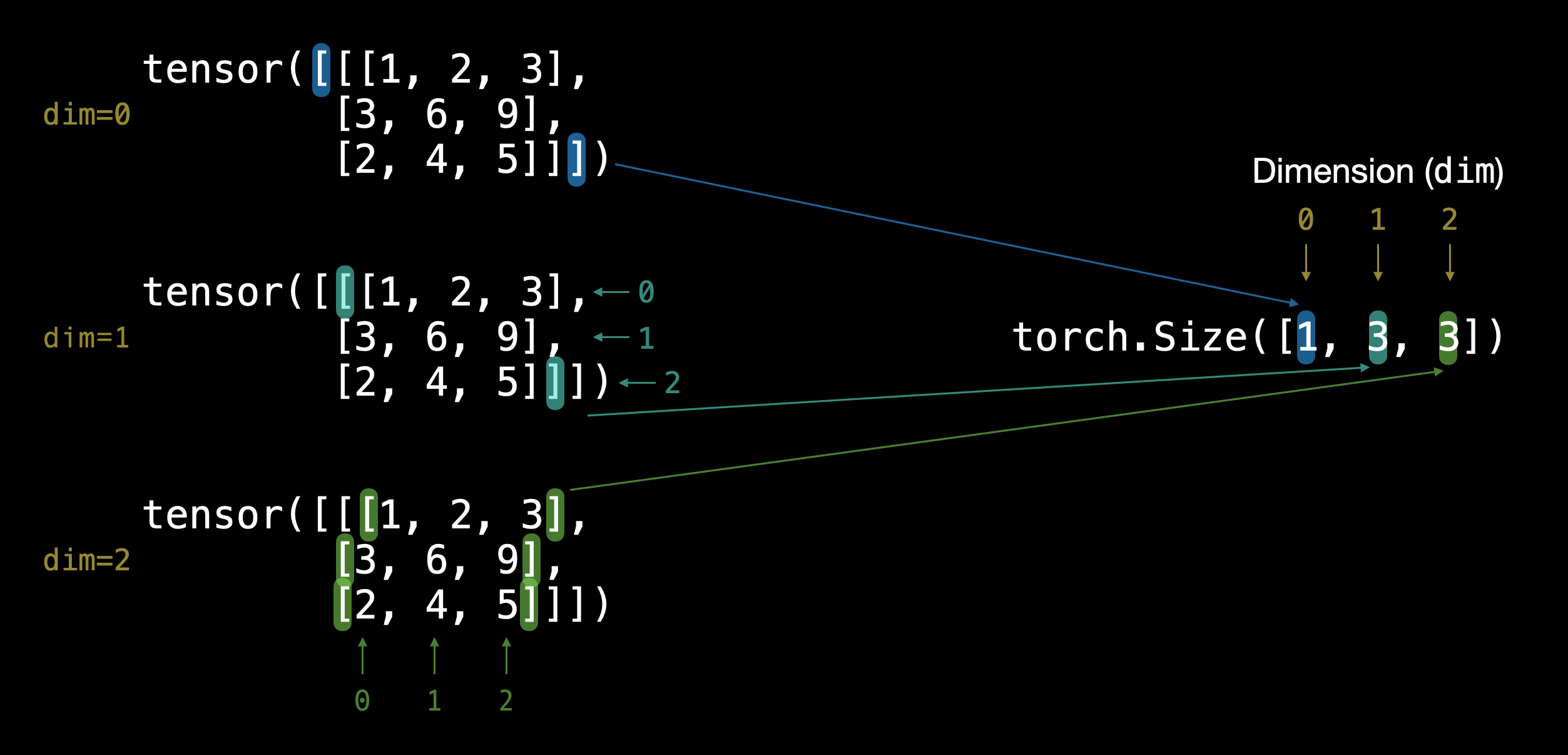
TENSOR = torch.tensor([[[1, 2, 3],
[3, 6, 9],
[2, 4, 5]]])
TENSOR
tensor([[[1, 2, 3],
[3, 6, 9],
[2, 4, 5]]])
The one we just created could be the sales numbers for a steak and almond butter store (two of my favourite foods).
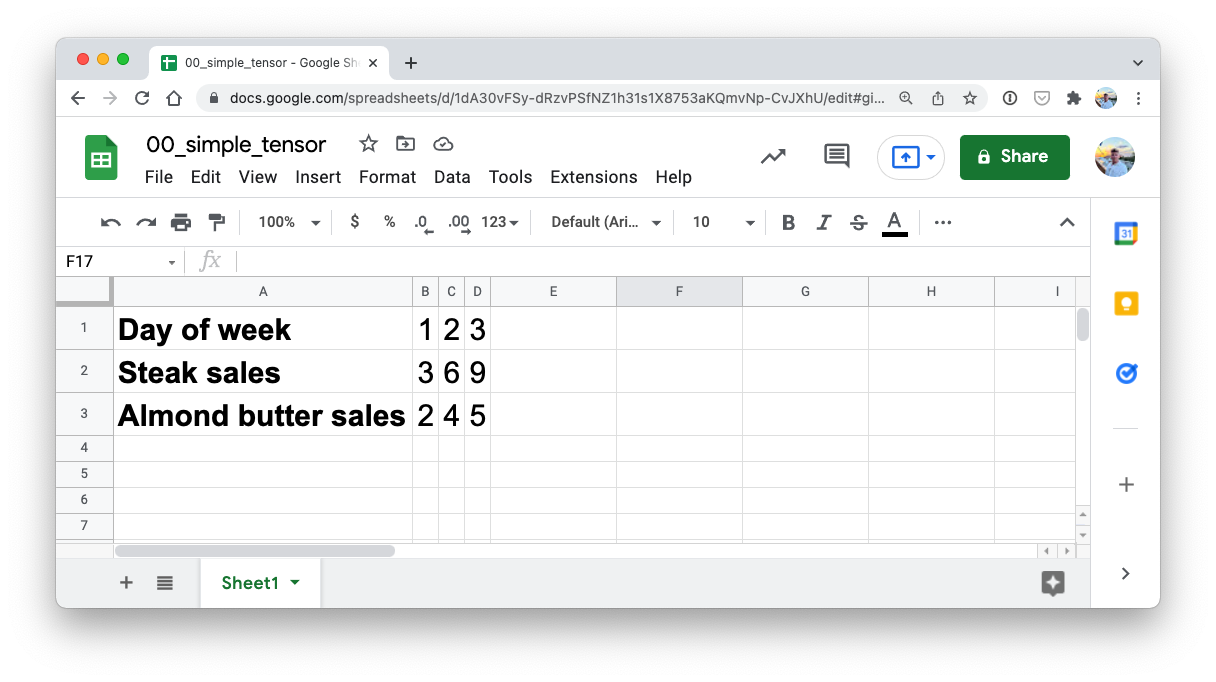
TENSOR.ndim, TENSOR.shape
(3, torch.Size([1, 3, 3]))
The dimensions go outer to inner.
That means there’s 1 dimension of 3 by 3.
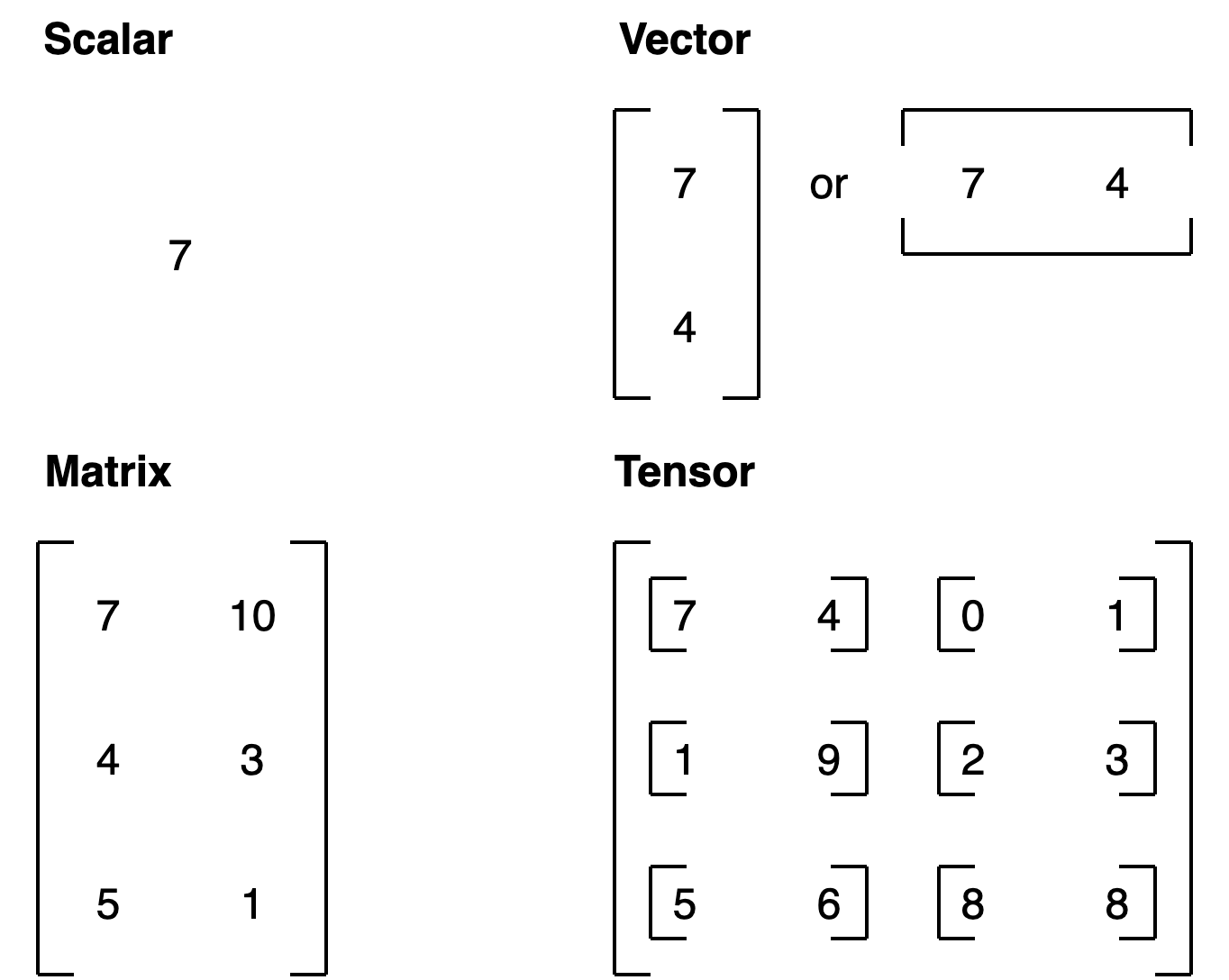
Note: You might’ve noticed me using lowercase letters for scalar and vector and uppercase letters for MATRIX and TENSOR. This was on purpose. In practice, you’ll often see scalars and vectors denoted as lowercase letters such as y or a. And matrices and tensors denoted as uppercase letters such as X or W.
You also might notice the names martrix and tensor used interchangably. This is common. Since in PyTorch you’re often dealing with torch.Tensor’s (hence the tensor name), however, the shape and dimensions of what’s inside will dictate what it actually is.
Random tensors
But when building machine learning models with PyTorch, it’s rare you’ll create tensors by hand (like what we’ve being doing).
Instead, a machine learning model often starts out with large random tensors of numbers and adjusts these random numbers as it works through data to better represent it.
In essence:
Start with random numbers -> look at data -> update random numbers -> look at data -> update random numbers…
# Create a random tensor of size (3, 4)
random_tensor = torch.rand(size=(3, 4))
random_tensor, random_tensor.dtype, random_tensor.shape , random_tensor.ndim
(tensor([[0.9638, 0.9171, 0.8510, 0.3581],
[0.7802, 0.7227, 0.5245, 0.0317],
[0.0926, 0.1394, 0.3519, 0.5473]]),
torch.float32,
torch.Size([3, 4]),
2)
The flexibility of torch.rand() is that we can adjust the size to be whatever we want.
For example, say you wanted a random tensor in the common image shape of [224, 224, 3] ([height, width, color_channels])
# Create a random tensor of size (224, 224, 3)
random_image_size_tensor = torch.rand(size=(224, 224, 3))
random_image_size_tensor.shape, random_image_size_tensor.ndim
(torch.Size([224, 224, 3]), 3)
random_image_size_tensor = torch.rand(size=(1, 3, 3))
random_image_size_tensor, random_image_size_tensor.ndim
(tensor([[[0.2242, 0.1729, 0.9013],
[0.7966, 0.1042, 0.0178],
[0.9993, 0.1032, 0.1653]]]),
3)
Zeros and ones
Sometimes you’ll just want to fill tensors with zeros or ones.
This happens a lot with masking (like masking some of the values in one tensor with zeros to let a model know not to learn them).
zeros = torch.zeros(size=(3, 4))
zeros, zeros.dtype
(tensor([[0., 0., 0., 0.],
[0., 0., 0., 0.],
[0., 0., 0., 0.]]),
torch.float32)
ones = torch.ones(size=(3, 4))
ones, ones.dtype
(tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.],
[1., 1., 1., 1.]]),
torch.float32)
# Create a range of values 0 to 10
zero_to_ten = torch.arange(start=0, end=10, step=1)
zero_to_ten
tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
# Can also create a tensor of zeros similar to another tensor
ten_zeros = torch.zeros_like(input=zero_to_ten) # will have same shape
ten_zeros
tensor([0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
Tensor datatypes
There are many different tensor datatypes available in PyTorch.
Some are specific for CPU and some are better for GPU.
Generally if you see torch.cuda anywhere, the tensor is being used for GPU (since Nvidia GPUs use a computing toolkit called CUDA).
The most common type (and generally the default) is torch.float32 or torch.float.
This is referred to as “32-bit floating point”.
But there’s also 16-bit floating point (torch.float16 or torch.half) and 64-bit floating point (torch.float64 or torch.double).
And to confuse things even more there’s also 8-bit, 16-bit, 32-bit and 64-bit integers.
Plus more!
Note: An integer is a flat round number like 7 whereas a float has a decimal 7.0.
The reason for all of these is to do with precision in computing.
Precision is the amount of detail used to describe a number.
The higher the precision value (8, 16, 32), the more detail and hence data used to express a number.
This matters in deep learning and numerical computing because you’re making so many operations, the more detail you have to calculate on, the more compute you have to use.
So lower precision datatypes are generally faster to compute on but sacrifice some performance on evaluation metrics like accuracy (faster to compute but less accurate).
# Default datatype for tensors is float32
float_32_tensor = torch.tensor([3.0, 6.0, 9.0],
dtype=None, # defaults to None, which is torch.float32 or whatever datatype is passed
device=None, # defaults to None, which uses the default tensor type
requires_grad=False) # if True, operations performed on the tensor are recorded
float_32_tensor.shape, float_32_tensor.dtype, float_32_tensor.device
(torch.Size([3]), torch.float32, device(type='cpu'))
Aside from shape issues (tensor shapes don’t match up), two of the other most common issues you’ll come across in PyTorch are datatype and device issues.
For example, one of tensors is torch.float32 and the other is torch.float16 (PyTorch often likes tensors to be the same format).
Or one of your tensors is on the CPU and the other is on the GPU (PyTorch likes calculations between tensors to be on the same device).
We’ll see more of this device talk later on.
For now let’s create a tensor with dtype=torch.float16.
float_16_tensor = torch.tensor([3.0, 6.0, 9.0],
dtype=torch.float16) # torch.half would also work
float_16_tensor.dtype
torch.float16
When you run into issues in PyTorch, it’s very often one to do with one of the three attributes above. So when the error messages show up, sing yourself a little song called “what, what, where”:
“what shape are my tensors? what datatype are they and where are they stored? what shape, what datatype, where where where”
Tensor Operations
In deep learning, data (images, text, video, audio, protein structures, etc) gets represented as tensors.
A model learns by investigating those tensors and performing a series of operations (could be 1,000,000s+) on tensors to create a representation of the patterns in the input data.
These operations are often a wonderful dance between:
Addition Substraction Multiplication (element-wise) Division Matrix multiplication And that’s it. Sure there are a few more here and there but these are the basic building blocks of neural networks.
Addition & Multiply
# Create a tensor of values and add a number to it
tensor = torch.tensor([1, 2, 3])
tensor + 10
tensor([11, 12, 13])
# Multiply it by 10
tensor * 10
tensor([10, 20, 30])
# Tensors don't change unless reassigned
tensor
tensor([1, 2, 3])
# Subtract and reassign
tensor = tensor - 10
tensor
tensor([-9, -8, -7])
# Can also use torch functions
torch.multiply(tensor, 10)
tensor([-90, -80, -70])
# Element-wise multiplication (each element multiplies its equivalent, index 0->0, 1->1, 2->2)
print(tensor, "*", tensor)
print("Equals:", tensor * tensor)
tensor([-9, -8, -7]) * tensor([-9, -8, -7])
Equals: tensor([81, 64, 49])
# torch.tensor([1, 2, 3]) * torch.tensor([1, 2])
# This will create an error ""the size of tensor a (3) must match the size of tensor b (2) at non-singleton dimension 0"
Matrix multiplication
Matrix multiplication (is all you need)
PyTorch implements matrix multiplication functionality in the torch.matmul() method.
The main two rules for matrix multiplication to remember are:
The inner dimensions must match: (3, 2) @ (3, 2) won’t work (2, 3) @ (3, 2) will work (3, 2) @ (2, 3) will work The resulting matrix has the shape of the outer dimensions: (2, 3) @ (3, 2) -> (2, 2) (3, 2) @ (2, 3) -> (3, 3)
tensor = torch.tensor([1, 2, 3])
tensor.shape
torch.Size([3])
# Element-wise matrix multiplication
tensor * tensor
tensor([1, 4, 9])
# Matrix multiplication
torch.matmul(tensor, tensor)
# torch.mm(tensor, tensor)
tensor(14)
# Can also use the "@" symbol for matrix multiplication, though not recommended
tensor @ tensor
tensor(14)
%%time
torch.matmul(tensor, tensor)
CPU times: user 150 µs, sys: 28 µs, total: 178 µs
Wall time: 128 µs
tensor(14)
One of the most common errors in deep learning (shape errors)
Because much of deep learning is multiplying and performing operations on matrices and matrices have a strict rule about what shapes and sizes can be combined, one of the most common errors you’ll run into in deep learning is shape mismatches.
# Shapes need to be in the right way
tensor_A = torch.tensor([[1, 2],
[3, 4],
[5, 6]], dtype=torch.float32)
tensor_B = torch.tensor([[7, 10],
[8, 11],
[9, 12]], dtype=torch.float32)
tensor_A.shape, tensor_B.shape
# torch.matmul(tensor_A, tensor_B) # (this will error)
(torch.Size([3, 2]), torch.Size([3, 2]))
# One of the ways to do this is with a transpose (switch the dimensions of a given tensor).
print(f"Original shapes: tensor_A = {tensor_A.shape}, tensor_B = {tensor_B.shape}\n")
print(f"New shapes: tensor_A = {tensor_A.shape} (same as above), tensor_B.T = {tensor_B.T.shape}\n")
print(f"Multiplying: {tensor_A.shape} * {tensor_B.T.shape} <- inner dimensions match\n")
print("Output:\n")
output = torch.matmul(tensor_A, tensor_B.T)
print(output)
print(f"\nOutput shape: {output.shape}")
Original shapes: tensor_A = torch.Size([3, 2]), tensor_B = torch.Size([3, 2])
New shapes: tensor_A = torch.Size([3, 2]) (same as above), tensor_B.T = torch.Size([2, 3])
Multiplying: torch.Size([3, 2]) * torch.Size([2, 3]) <- inner dimensions match
Output:
tensor([[ 27., 30., 33.],
[ 61., 68., 75.],
[ 95., 106., 117.]])
Output shape: torch.Size([3, 3])
# torch.mm is a shortcut for matmul
# A matrix multiplication like this is also referred to as the dot product of two matrices.
torch.mm(tensor_A, tensor_B.T)
tensor([[ 27., 30., 33.],
[ 61., 68., 75.],
[ 95., 106., 117.]])
Neural networks are full of matrix multiplications and dot products.
The torch.nn.Linear() module (we’ll see this in action later on), also known as a feed-forward layer or fully connected layer, implements a matrix multiplication between an input x and a weights matrix A.
y= x⋅AT+b
Where:
x is the input to the layer (deep learning is a stack of layers like torch.nn.Linear() and others on top of each other). A is the weights matrix created by the layer, this starts out as random numbers that get adjusted as a neural network learns to better represent patterns in the data (notice the “T”, that’s because the weights matrix gets transposed). Note: You might also often see W or another letter like X used to showcase the weights matrix. b is the bias term used to slightly offset the weights and inputs. y is the output (a manipulation of the input in the hopes to discover patterns in it). This is a linear function (you may have seen something like \(y = mx+b\) in high school or elsewhere), and can be used to draw a straight line!
Let’s play around with a linear layer.
Try changing the values of in_features and out_features below and see what happens.
Do you notice anything to do with the shapes?
tensor_A
tensor([[1., 2.],
[3., 4.],
[5., 6.]])
# Since the linear layer starts with a random weights matrix, let's make it reproducible (more on this later)
torch.manual_seed(42)
# This uses matrix multiplication
linear = torch.nn.Linear(in_features=2, # in_features = matches inner dimension of input
out_features=6) # out_features = describes outer value
x = tensor_A
output = linear(x)
print(f"Input shape: {x.shape}\n")
print(f"Output:\n{output}\n\nOutput shape: {output.shape}")
Input shape: torch.Size([3, 2])
Output:
tensor([[2.2368, 1.2292, 0.4714, 0.3864, 0.1309, 0.9838],
[4.4919, 2.1970, 0.4469, 0.5285, 0.3401, 2.4777],
[6.7469, 3.1648, 0.4224, 0.6705, 0.5493, 3.9716]],
grad_fn=<AddmmBackward0>)
Output shape: torch.Size([3, 6])
# Finding the min, max, mean, sum
x = torch.arange(0, 100, 10)
x
tensor([ 0, 10, 20, 30, 40, 50, 60, 70, 80, 90])
print(f"Minimum: {x.min()}")
print(f"Maximum: {x.max()}")
# print(f"Mean: {x.mean()}") # this will error
print(f"Mean: {x.type(torch.float32).mean()}") # won't work without float datatype
print(f"Sum: {x.sum()}")
Minimum: 0
Maximum: 90
Mean: 45.0
Sum: 450
torch.max(x), torch.min(x), torch.mean(x.type(torch.float32)), torch.sum(x)
(tensor(90), tensor(0), tensor(45.), tensor(450))
Positional min/max
You can also find the index of a tensor where the max or minimum occurs with torch.argmax() and torch.argmin() respectively.
This is helpful incase you just want the position where the highest (or lowest) value is and not the actual value itself (we’ll see this in a later section when using the softmax activation function).
# Create a tensor
tensor = torch.arange(10, 100, 10)
print(f"Tensor: {tensor}")
# Returns index of max and min values
print(f"Index where max value occurs: {tensor.argmax()}")
print(f"Index where min value occurs: {tensor.argmin()}")
Tensor: tensor([10, 20, 30, 40, 50, 60, 70, 80, 90])
Index where max value occurs: 8
Index where min value occurs: 0
Reshaping, stacking, squeezing and unsqueezing
Because deep learning models (neural networks) are all about manipulating tensors in some way. And because of the rules of matrix multiplication, if you’ve got shape mismatches, you’ll run into errors. These methods help you make the right elements of your tensors are mixing with the right elements of other tensors.
x = torch.arange(1., 8.)
x, x.shape
(tensor([1., 2., 3., 4., 5., 6., 7.]), torch.Size([7]))
# Add an extra dimension
x_reshaped = x.reshape(1, 7)
x_reshaped, x_reshaped.shape
(tensor([[1., 2., 3., 4., 5., 6., 7.]]), torch.Size([1, 7]))
z = x.view(1, 7)
z, z.shape
(tensor([[1., 2., 3., 4., 5., 6., 7.]]), torch.Size([1, 7]))
Remember though, changing the view of a tensor with torch.view() really only creates a new view of the same tensor.
So changing the view changes the original tensor too.
# Changing z changes x
z[:, 0] = 5
z, x
(tensor([[5., 2., 3., 4., 5., 6., 7.]]), tensor([5., 2., 3., 4., 5., 6., 7.]))
# if we wanted to stack our new tensor on top of itself five times, we could do so with torch.stack().
# Stack tensors on top of each other
x_stacked = torch.stack([x, x, x, x], dim=0) # try changing dim to dim=1 and see what happens
x_stacked
tensor([[5., 2., 3., 4., 5., 6., 7.],
[5., 2., 3., 4., 5., 6., 7.],
[5., 2., 3., 4., 5., 6., 7.],
[5., 2., 3., 4., 5., 6., 7.]])
How about removing all single dimensions from a tensor?
To do so you can use torch.squeeze() (I remember this as squeezing the tensor to only have dimensions over 1).
print(f"Previous tensor: {x_reshaped}")
print(f"Previous shape: {x_reshaped.shape}")
# Remove extra dimension from x_reshaped
x_squeezed = x_reshaped.squeeze()
print(f"\nNew tensor: {x_squeezed}")
print(f"New shape: {x_squeezed.shape}")
Previous tensor: tensor([[5., 2., 3., 4., 5., 6., 7.]])
Previous shape: torch.Size([1, 7])
New tensor: tensor([5., 2., 3., 4., 5., 6., 7.])
New shape: torch.Size([7])
# And to do the reverse of torch.squeeze() you can use torch.unsqueeze() to add a dimension value of 1 at a specific index.
print(f"Previous tensor: {x_squeezed}")
print(f"Previous shape: {x_squeezed.shape}")
## Add an extra dimension with unsqueeze
x_unsqueezed = x_squeezed.unsqueeze(dim=0)
print(f"\nNew tensor: {x_unsqueezed}")
print(f"New shape: {x_unsqueezed.shape}")
Previous tensor: tensor([5., 2., 3., 4., 5., 6., 7.])
Previous shape: torch.Size([7])
New tensor: tensor([[5., 2., 3., 4., 5., 6., 7.]])
New shape: torch.Size([1, 7])
You can also rearrange the order of axes values with torch.permute(input, dims), where the input gets turned into a view with new dims.
# Create tensor with specific shape
x_original = torch.rand(size=(224, 224, 3))
# Permute the original tensor to rearrange the axis order
x_permuted = x_original.permute(2, 0, 1) # shifts axis 0->1, 1->2, 2->0
print(f"Previous shape: {x_original.shape}")
print(f"New shape: {x_permuted.shape}")
Previous shape: torch.Size([224, 224, 3])
New shape: torch.Size([3, 224, 224])
Indexing
Sometimes you’ll want to select specific data from tensors (for example, only the first column or second row).
x = torch.arange(1, 10).reshape(1, 3, 3)
x, x.shape
(tensor([[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]]),
torch.Size([1, 3, 3]))
Indexing values goes outer dimension -> inner dimension (check out the square brackets).
# Let's index bracket by bracket
print(f"First square bracket:\n{x[0]}")
print(f"Second square bracket: {x[0][0]}")
print(f"Third square bracket: {x[0][0][0]}")
First square bracket:
tensor([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
Second square bracket: tensor([1, 2, 3])
Third square bracket: 1
You can also use : to specify “all values in this dimension” and then use a comma (,) to add another dimension.
x[:]
tensor([[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]])
x[:,:,:,]
tensor([[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]])
# Get all values of 0th dimension and the 0 index of 1st dimension
x[:, 0]
tensor([[1, 2, 3]])
# Get all values of 0th & 1st dimensions but only index 1 of 2nd dimension
x[:, :, 1]
tensor([[2, 5, 8]])
# Get all values of the 0 dimension but only the 1 index value of the 1st and 2nd dimension
x[:, 1, 1]
tensor([5])
# Get index 0 of 0th and 1st dimension and all values of 2nd dimension
x[0, 0, :] # same as x[0][0]
tensor([1, 2, 3])
Pytorch Best Practise
You can also use torch.as_tensor() to convert a numpy array to a torch tensor, This will not create a new copy of the data
a = np.random.rand(3, 3)
# Bad way
t1 = torch. tensor(a)
# Good way
t2 = torch.as_tensor(a)
t3 = torch.from_numpy(a)
Avoid cpu, item() these will use functions to tranfer data between devices
t= torch.rand(2,2)
# bad way
t.cpu ()
t[0][0].item()
t. numpy ()
# good way
t.detach ()
tensor([[0.8016, 0.3649],
[0.6286, 0.9663]])
Create tensor direclty on GPU
# bad way
# t = torch.rand(2,2).cuda()
# good way
# t = torch. rand(2,2, device="cuda")