Greedy Algorithms

Divide and Conquer

Divide and conquer is a general algorithm design paradigm: divide the problem into smaller subproblems, solve the subproblems recursively, and then combine the solutions to the subproblems to solve the original problem.

Largest pair sum in an unsorted array

Given an unsorted of distinct integers, find the largest pair sum in it. For example, the largest pair sum in {12, 34, 10, 6, 40} is 74.

Brute force solution

numbers = [2,1,0,8,15,7,-1,6]
print(numbers)

max_pair_sum = 0

for i in numbers:
    for j in numbers:
        if i != j:
            max_pair_sum = max(max_pair_sum, i + j)

print(max_pair_sum)

# time Complexity = n^2
# space Complexity = 1

[2, 1, 0, 8, 15, 7, -1, 6]
23

Best solution

1. Initialize the first = Integer.MIN_VALUE second = Integer.MIN_VALUE

2. Loop through the elements a) If the current element is greater than the first max element, then update second max to the first max and update the first max to the current element.

3. Return (first + second)

def findLargestSumPair(arr, n):
 
    # Initialize first and second
    # largest element
    if arr[0] > arr[1]:
        first_big_number = arr[0]
        second_big_number = arr[1]
 
    else:
        first_big_number = arr[1]
        second_big_number = arr[0]
 
    # Traverse remaining array and
    # find first and second largest
    # elements in overall array
    for i in range(2, n):
 
        # If current element is greater
        # than first then update both
        # first and second
        if arr[i] > first_big_number:
            second_big_number = first_big_number
            first_big_number = arr[i]
 
        # If arr[i] is in between first
        # and second then update second
        elif arr[i] > second_big_number and arr[i] != first_big_number:
            second_big_number = arr[i]
 
    return (first_big_number , second_big_number)

first, second = findLargestSumPair(numbers, len(numbers))

print(first, second)

print(first + second)

# time Complexity = n
# space Complexity = 1

15 8
23

Max subarray problem

Given an array of integers, find the contiguous subarray that has the largest sum. Return the sum.

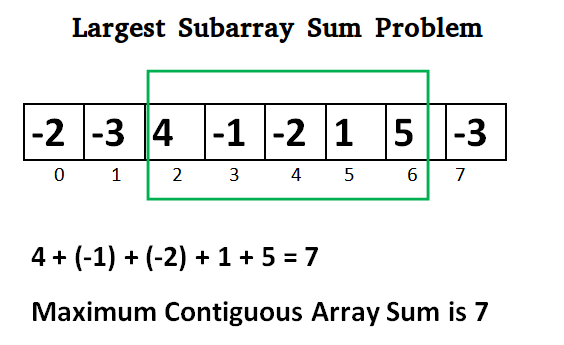
Brute force solution

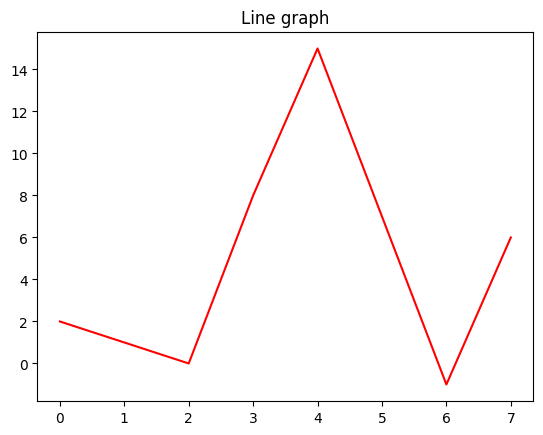
Draw graph which show as stock values.

import numpy as np
import matplotlib.pyplot as plt

numbers = [2,1,0,8,15,7,-1,6]
print(numbers)

x = range(len(numbers))
y = numbers

plt.title("Line graph")
plt.plot(x, y, color="red")

plt.show()

[2, 1, 0, 8, 15, 7, -1, 6]

max_contiguous_sum = 0

for index,v in enumerate(numbers):
    for j in range(index ,len(numbers)):
        # print(index, j)
        # print(numbers[index:j+1])
        max_contiguous_sum = max(max_contiguous_sum, sum(numbers[index:j+1]))
        
print(max_contiguous_sum)

38

Divide and Conquer solution

import sys

def maxSubArraySum(arr):
    # Base case: when there is only one element in the array
    if len(arr) == 1:
        return arr[0]
 
    # Recursive case: divide the problem into smaller sub-problems
    m = len(arr) // 2
 
    # Find the maximum subarray sum in the left half
    left_max = maxSubArraySum(arr[:m])
 
    # Find the maximum subarray sum in the right half
    right_max = maxSubArraySum(arr[m:])
 
    # Find the maximum subarray sum that crosses the middle element
    left_sum = -sys.maxsize - 1
    right_sum = -sys.maxsize - 1
    sum = 0
 
    # Traverse the array from the middle to the right
    for i in range(m, len(arr)):
        sum += arr[i]
        right_sum = max(right_sum, sum)
 
    sum = 0
 
    # Traverse the array from the middle to the left
    for i in range(m - 1, -1, -1):
        sum += arr[i]
        left_sum = max(left_sum, sum)
 
    cross_max = left_sum + right_sum
 
    # Return the maximum of the three subarray sums
    return max(cross_max, max(left_max, right_max))

print(maxSubArraySum(numbers))

38

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

def max_subarray(arr):
    if len(arr) == 1:
        return arr[0]
    else:
        mid = len(arr) // 2
        left = max_subarray(arr[:mid])
        right = max_subarray(arr[mid:])
        cross = max_crossing_subarray(arr, mid)
        return max(left, right, cross)

def max_crossing_subarray(arr, mid):
    left_sum = -np.inf
    right_sum = -np.inf
    sum = 0
    for i in range(mid - 1, -1, -1):
        sum += arr[i]
        if sum > left_sum:
            left_sum = sum
            max_left = i
    sum = 0
    for j in range(mid, len(arr)):
        sum += arr[j]
        if sum > right_sum:
            right_sum = sum
            max_right = j
    return left_sum + right_sum

arr = np.random.randint(-10, 10, 10)
arr = np.array(numbers)

max_subarray(arr)

38

def max_subarray(arr):
    max_sum = -np.inf
    for i in range(len(arr)):
        sum = 0
        for j in range(i, len(arr)):
            sum += arr[j]
            if sum > max_sum:
                max_sum = sum
                max_left = i
                max_right = j
    return max_sum

max_subarray(arr)

38

Fast Fourier Transform Algorithm